Autor: Lukas Raffl
Titel: Bauwerksüberwachung mit scannenden Tachymetern
Art: Master's Thesis
Jahr, Nr.: 2017, #438
Betreuer: Dr.-Ing. Andreas Wagner

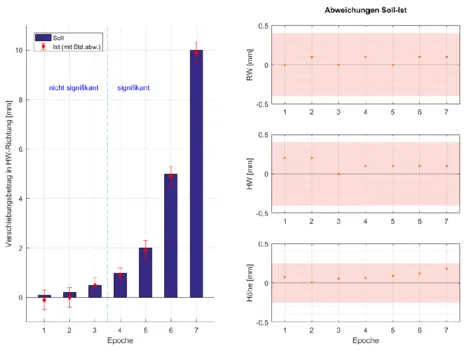
In dieser Arbeit wird ein neues Verfahren zur Bauwerksüberwachung mittels scannender Tachymeter vorgestellt. Deren integrierte Scanning-Funktion ermöglicht den teilweisen Verzicht auf signalisierte Zielpunkte. Das Verfahren basiert auf dem gezielten Scanning wiederauffindbarer Fassadenstrukturen, aus denen homologe Punkte über alle Epochen extrahiert werden können. Es werden zwei Methoden präsentiert, anhand derer sich aus den Bereichsscans eindeutige, nichtsignalisierte Zielpunkte ableiten lassen. Die Hauptmethode beruht auf der Modellierung und Verschneidung dreier Ebenen an einer Fensterecke zu einem fiktiven Punkt, zu dem sich eine tachymetrische Pseudobeobachtung erzeugen lässt. Alternativ dazu können auch mittels ICP-Algorithmus (Iterative Closest Point) korrespondierende Pseudobeobachtungen pro Epoche generiert werden. Die so erhaltenen fiktiven Messungen werden anschließend im Sinne einer hybriden Auswertung zu den Tachymetriedaten hinzugefügt und in eine strenge Deformationsanalyse mit Signifikanzaussage integriert. Da die in Frage kommenden Scanbereiche bestimmte Voraussetzungen erfüllen müssen, wird außerdem ein entsprechender Evaluierungsalgorithmus etabliert. Die Validierung dieses neuartigen Überwachungskonzepts erfolgte im Rahmen eines Laborversuches, wobei im gescannten, nicht-signalisierten Zielpunkt signifikante Deformationen bereits ab einer Verschiebung von einem Millimeter nachgewiesen werden konnten. Die Anwendung auf reale Fassadenscans beweist ebenfalls, dass das Verfahren zuverlässige Ergebnisse liefert und die abgeschätzte Genauigkeit zutreffend ist. Auch die automatisierte Evaluierung gibt gültige Bewertungen aus und ermöglicht eine sichere Auswahl geeigneter Scanbereiche. Das vorgestellte Verfahren für scannende Tachymeter hat folglich großes Potential und bietet zudem einige Erweiterungsmöglichkeiten, wie z. B. die Integration der bildgebenden Funktion.